科拉茨猜想-用數學看到潛在的世界規律
這種數學相關的文章莫名的吸引我,
我一直懷疑,關於我們活在Matrix中的證明,就藏在數學中。
科拉茨猜想所得到相關的數字規律,看起來像是許多事物的常態分佈,像是冰雹融化的過程、國家的人口數、公司的市值、珊瑚的結構、海藻的形狀。
全文連結:
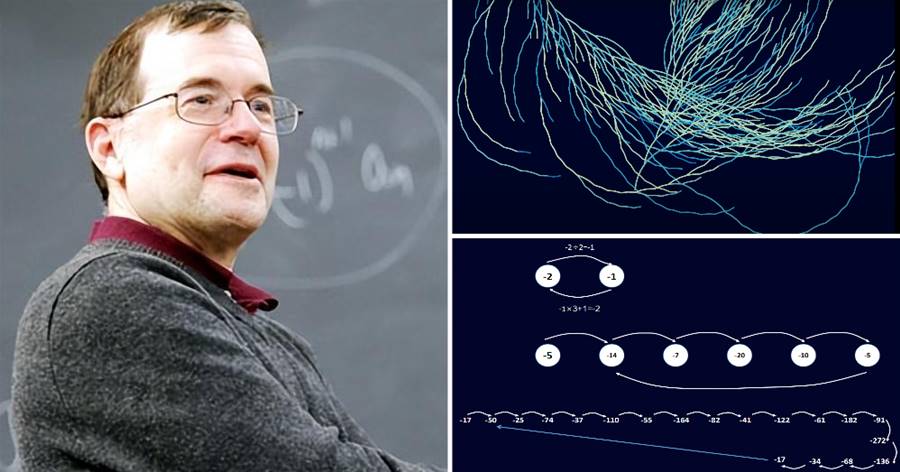
文章摘要:
這個問題的核心內容是這樣的:從任意一個正整數開始,如果這個數是偶數,就將其除以2;如果是奇數,則乘以3再加1。然后對所得的結果重復以上步驟。關于這個問題的猜想認為,無論我們從哪個正整數出發,最終都會達到數字1(進入一個4,2,1的循環)。(原文摘要)
這個猜想被稱為 **科拉茨猜想**(Collatz conjecture),也被稱為 **3X+1猜想**。通過應用3x+1得到的數字被稱為 **冰雹數(hailstone numbers)**,因為它們像雷暴云中的冰雹一樣上下起伏,但最終都會降到1。(原文摘要)
研究了冰雹數的路徑,看是否有規律。顯然,所有數最終都會回到1, **但是它們回到1的過程如何呢?模式是隨機的**。(原文摘要)
這并非巧合,它是 **幾何布朗運動**的例子。這意味著,如果取對數并消除線性趨勢,波動是隨機的。(原文摘要)
這種模式不是3x+1獨有的,實際上它在各個領域都有出現,從國家人口到公司價值,以及物理常數和斐波那契數列等等。
(原文摘要)這種分布被稱為 **本福特定律(**benford‘slaw **)**,它甚至可以用于 **檢測欺詐**。如果你的所得稅表格上的所有數字都符合本福特定律,那麼你可能是誠實的;如果不符合,你可能在隱藏一些事情。在選舉中,本福特定律可用于發現違規行為。
(原文摘要)一些數學家通過將每個數字逆時針旋轉(如果是奇數)和順時針旋轉(如果是偶數)來修改這種可視化。然后你得到一個看起來像珊瑚或海藻的結構。通過調整奇數和偶數的旋轉角度,你可以創建出這些美麗的有機形狀。
(原文摘要)訂閱電子報
輸入Email訂閱最新內容電子報

